
\(f(x) + a\) represents a translation through the vector \(\begin\). If \(a\) is negative, the graph translates downwards. If \(a\) is positive, the graph translates upwards.
The flip is performed over the line of reflection. The addition of the value \(a\) represents a vertical translation in the graph. We will discuss two types of reflections: reflections across the x-axis and reflections across the y-axis. TRANSFORMATIONS CHEAT-SHEET REFLECTIONS: Reflections are a flip. Here we are adding \(a\) to the whole function. Translations are when we shift the entire graph. If \(f(x) = x^2\), then \(f(x) + a = x^2 + a\). There are three types of transformations which we will be dealing with: translations, dilations and reflections. The different figures in mathematics can be reflected. the origin x y J Z L 2) translation: 4 units right and 1 unit down x y Y F G 3) translation: 1 unit right and 1 unit up x y E J T M 4) reflection across the x-axis x y M C J K Write a rule to describe each transformation. What is a reflection over the x-axis Firstly, a reflection is a type of transformation representing the flip of a point, line, or curve. Writing graphs as functions in the form \(f(x)\) is useful when applying translations and reflections to graphs. All Transformations Date Period Graph the image of the figure using the transformation given. Clearly, the y-values of y f(x) must be opposite in sign to the y-values of y f(x). Note how the minus sign appears on the outside of the function. The graph of \(f(x) = x^2\) is the same as the graph of \(y = x^2\). In the previous section, we were asked to draw the graph of y f(x). Note: there are no method marks awarded for any transformation questions no matter how many marks are being awarded, they are all answer marks.ĭilation from the x-axis by a factor of aĭilation from the y-axis by a factor of aĮxample 3.A translation is a movement of the graph either horizontally parallel to the \(x\) -axis or vertically parallel to the \(y\) -axis. In methods we are generally concerned with - reflections in the x-axis, y-axis and line y=x Reflections simply flip the graph relative to a certain line. All dilation factors are positive.Ī dilation from the y-axis by a factor larger than one ( > 1) will result in the graph being stretched away from the y-axis.Ī dilation from the y-axis by a factor less than one ( 1) will result in the graph being stretched away from the x-axis.Ī dilation from the x-axis by a factor less than one ( < 1) will result in the graph being compressed towards the x-axis. Transformation of f(c>0) f ( c > 0) Effect on the graph off f. Graphic designers and 3D modellers use transformations of graphs to design objects and images. To graph a reflection, you can visualize what. We can summarize the different transformations and their related effects on the graph of a function in the following table. Functions of graphs can be transformed to show shifts and reflections. Reflections are opposite isometries, something we will look below. Conceptually, a reflection is basically a flip of a shape over the line of reflection.

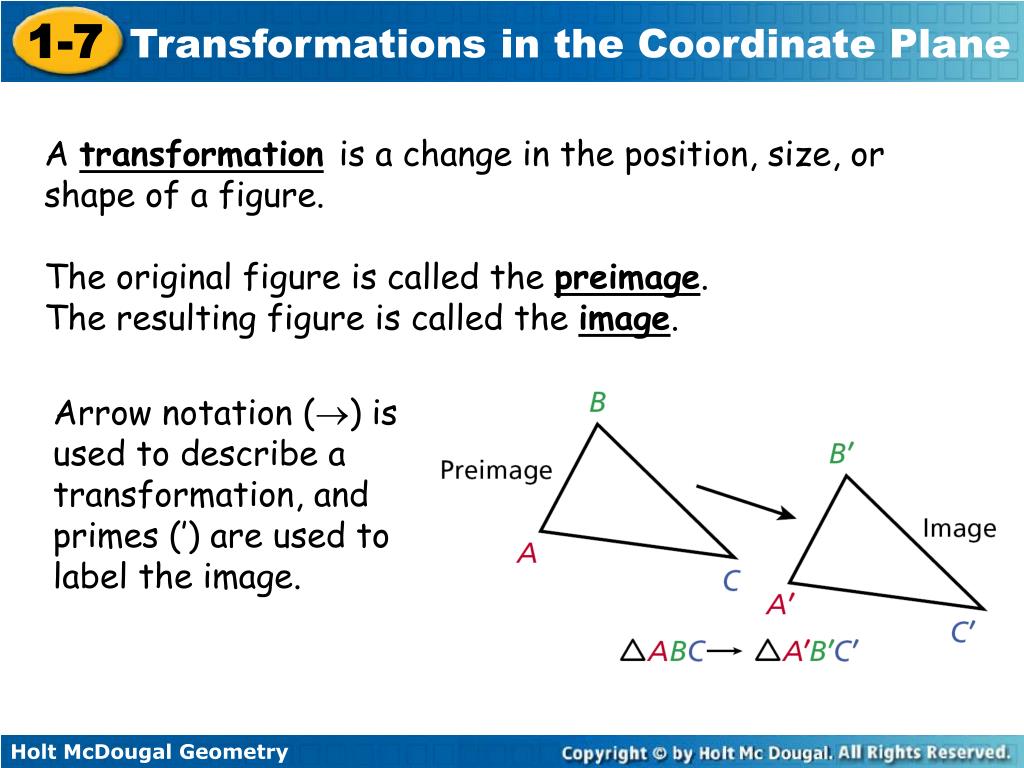
A reflection is an example of a transformation that takes a shape (called the preimage) and flips it across a line (called the line of reflection) to create a new shape (called the image). A reflection is a kind of transformation. In other words, imagine folding the graph of the function over the y-axis. Translations are when we shift the entire graph left, right, up or down.ĭilations stretch or compress the graph. In geometry, a transformation is an operation that moves, flips, or changes a shape to create a new shape. In geometry, a reflection is a rigid transformation in which an object is. There are three types of transformations which we will be dealing with: translations, dilations and reflections. /rebates/2fhotmath2fhotmathhelp2ftopics2ftransformations-of-graphs&.


 0 kommentar(er)
0 kommentar(er)
